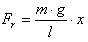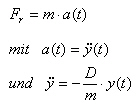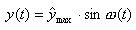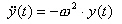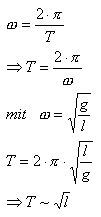Abhängigkeit der Frequenz von der Auslenkhöhe( SEK I und SEK II )
Abhängigkeit der Frequenz von der Masse ( SEK I und SEK II )
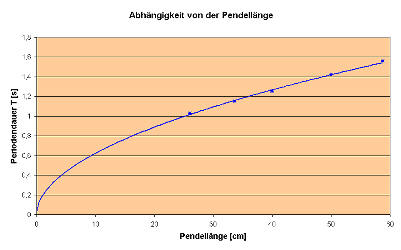
Abhängigkeit der Frequenz von der Fadenlänge ( SEK I und SEK II )
Herleitung der Formel (nur SEK II )
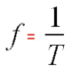



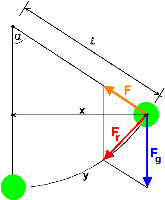 |
Auf das Pendel wirken die Gewichtskraft Fg und die Fadenkraft
ein. Die daraus resultierende Kraft Fr wird durch das
Kräfteparallelogramm gebildet. Die Größe von Fr ist
abhängig vom Winkel α. |
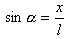
Daraus folgt für die resultiernde Kraft Fr